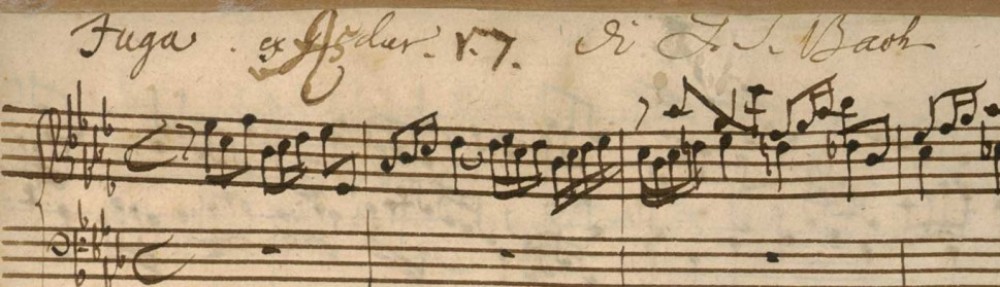A Prime Example of an Eleven Note Composition

The Prelude and Fugue in C Major

from the First Volume of the Well-Tempered Clavier by J. S. Bach.

http://rodneymills.com/th1s_1s_a_4o4.html The awareness of this overriding eleven-pitch-class sensitivity becomes more evident in examining compositions such as the Prelude and Fugue in C major from the first volume of the Well-Tempered Clavier by J. S. Bach.  The fugue is the “perfect” eleven-note piece:  It employs all the notes of the chromatic scale except for pc 3; there isn’t a single D-sharp or E-flat present at all while all the other notes are present.

buy Lyrica belfast  

The prelude, however, creates a new problem:  There are only two instances of  E-flat, but every time it is present, there is an F-sharp present simultaneously as part of a diminished seventh sonority.  Why?

The Action of System Modulation

When Bach introduces E-flat, a new eleven-note system becomes operational, and so, one must assume a transposition from a 0 system to the first occurrence of a system obtained by the introduction of E-flat, a 3-flat system.  If one considers this along the circle of fifths, you will note that, by moving counterclockwise along the circle from C major, E-flat is the first opportunity where all the notes of C minor are present, although reordered.  In the key of E-flat major (or C minor, for that matter), the missing pitch is F-sharp.  So, the missing pitch spelled as a “flat” (a minor third above the tonic of the major mode) propels the systems in a flat, counterclockwise manner, by three keys.  If the missing pitch were spelled as a “sharp” (an augmented second above the tonic of the major mode), the opposite would have to occur.  So, from the viewpoint of E-flat major, the augmented second above E-flat is F-sharp, moving the systems clockwise and back to a 0 system.

Short Term Modulation or System Conflict

So, why does Bach consistently employ an F-sharp after he has invoked the system of the parallel minor by using an E-flat in the C major prelude?  Simply to avoid a system modulation.  E-flat would have accomplished a system modulation to 3 flats had F-sharp not been present.  Bach is “sensitive” to the eleven-note issue but needs to find a way of using the twelfth “missing pitch” without ignoring the basic fabric of music as he had been taught it.  Haydn basically follows the same scheme in the first movement of his C major Symphony no. 82 (“The Bear”) where he introduces an E-flat in m. 30 and then succeeds it, in m. 33, with F-sharp.  The missing pitch of the tonic and missing pitch of the alternative system do not occur simultaneous, as they do in Bach, but they are very close, so the arrival at the 3-flat system is there but quite short-lived.

Longer Term Modulation

Of course, the process can easily be altered so that the composer could spend some time in an alternative eleven-pitch-class system before returning to the tonic system (see the Mozart example below).  A contemporary of Bach, Antonio Vivaldi, would sometimes introduce the parallel minor in a major-mode composition (with the use of a piano idée) and not “compensate” for the difference, even at the end.  A potential conflict between the key and the system is not particularly unusual, especially as we approach the Classical era, and these conflicting palettes will become a compositional hot potato with composers such as Beethoven.  Another potential alteration can be seen by introducing the missing pitch of the tonic key, but then introducing the missing pitch of the alternative system as a flat.  So, in C major, the introduction of E-flat moves us into a 3-flat system; but then the introduction of the missing pitch of the 3-flat system spelled as G-flat (see the matrix diagram above) would propel us further down, this time into a 6-flat system.  Returning to a 0 system is accomplished in two steps, first with the use of an A-natural to return the 6-flat system to a 3 flats, and then with an F-sharp to return us to a 0 system.

QUESTIONS? Please send us your questions and comments. We would love to discuss them further with you.

A simple musical example might help to illustrate how one may attain new insights into the compositional process by analyzing the PCA and assuming an eleven-pitch class sensitivity on the part of composers.  We shall utilize Mozart’s  concise choral work, Ave verum corpus, K. 618 in order to demonstrate how the PCA and systems analysis can elucidate Mozart’s developmental process.

Click Here for a complete systems analysis of this work by Mozart.